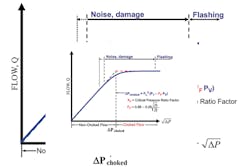
Liquid choked flow in control valves results in either flashing, or more often, cavitation. The classical approach to explaining choked flow is by assuming that flow increases linearly with the square root of pressure drop, ∆P, until ∆P reaches the choked pressure drop, ∆Pchoked, and then immediately becomes fully choked with no further increase in flow. (See the dashed lines in Figure 1.) The term used here for the dividing line between nonchoked flow and choked flow (∆Pchoked) is the terminology used in the 2012 version of the International Society of Automation (ISA) control valve sizing equation standard. Prior to that, the dividing line was not given a name, so valve manufacturers made up names. Some examples are ∆Pallowable, ∆Pterminal, ∆Pmax and ∆Pcritical. In reality, there is a certain amount of rounding out of the graph at the ∆Pchoked point, as shown in Figure 1.
Figure 2. Geometry of the valve orifice influences the length of the transition from nonchoked to fully choked flow.
The choking curve shape is influenced by the valve orifice geometry. As an example, see the segment ball valve in Figure 2, which has a significant choking transition curve. For the segment ball valve, the choking range has a significant transition region because of the configuration of the flow passage. The segment valve has an irregularly shaped flow area. The restricted flow at the narrow ends of the irregularly shaped area creates locally higher shear stresses, which causes cavitation (and eventually choking) to first occur in these regions. Eventually the entire area will choke as the pressure drop across the valve increases. As a result of the nonuniform distribution of cavitation potential, choking occurs in different locations inside the valve at different flow rates. This causes the choking transition region.
In contrast to the segment ball valve, the globe valve has a very symmetrical flow area, so choking will start at approximately all points in the flow path at the same time, resulting in a much shorter transition region between nonchoked flow and fully choked flow.1
Flow curve complications
No recognized method for calculating the shape of the rounded portion of the graph exists, so the ISA equations plot the dashed lines in Figure 1. For years the classical approach (dashed lines) was used for predicting cavitation damage. The assumption was that if the actual pressure drop was less than ∆Pchoked, there was no cavitation damage and if the actual pressure drop was greater than ∆Pchoked, then cavitation damage was present. In recent years, most control valve users and manufacturers have recognized that operating too close to the ∆Pchoked point can result in unacceptable levels of cavitation damage. It is not uncommon to find mechanical damage caused by the vibration that results from cavitation. The author recalls an instance where the bolts attaching an actuator to the valve had loosened to the point that the actuator flopped around and was about ready to fall off. In another instance, an electric motor-operated isolation valve about 20 feet downstream of a cavitating valve had failed. The motor capacitor had failed because of the high vibration.
This flow curve rounding makes predicting damage more complicated than comparing the actual pressure drop with the calculated choked pressure drop (which assumes the classical discussion of a sudden transition between nonchoked flow and choked flow). Noise and damage can begin before pressure in the main flow stream at the vena contracta drops to FF PV (FF times the vapor pressure of the liquid). Though many published discussions of choked flow, cavitation and flashing talk about vena contracta pressure dropping to the vapor pressure, numerous choked flow tests have shown that pressure at the vena contracta must drop below the upstream vapor pressure for vaporization to take place in the vena contracta and for flow to choke. The ISA formula in Figure 1 for FF gives a good approximation of how much below the upstream vapor pressure the vena contracta pressure must drop for flow to choke.
Figure 3. Cavitation can begin when the vena contracta pressure is above FFPV.
Cavitation stages
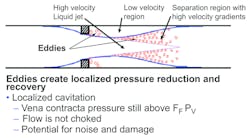
The first stages of cavitation begin when the average pressure in the main flow jet at the vena contracta is still above FF times the vapor pressure of the liquid (see Figure 3). At points of abrupt increase in flow area, the streamlines that are attached to the physical boundaries of the valve can separate and when they do, they form vortices or eddies. The rotational velocity in the eddies can be high enough that the local pressure inside an eddy drops below the vapor pressure and vapor bubbles form. As the eddy’s rotational velocity decreases, the pressure surrounding the vapor bubbles increases and the bubbles collapse. Vortices also form in the shear layer adjacent to the main jet where high-velocity gradients exist, and these are also potential sources for cavitation.
This level of cavitation has the potential for generating noise and causing damage even before the flow curve starts to deviate from a straight line.
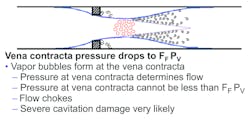
As the pressure drop across the valve increases, the velocity at the vena contracta increases and the pressure at the vena contracta drops to FFPV (see Figure 4).
Figure 4. Vena contracta pressure drops to FFPV.
The flow through a control valve depends on the pressure at the vena contracta. Since it is impossible for the pressure at the vena contracta to be less than FF times the vapor pressure of the liquid, the flow becomes choked; that is, further decreases in downstream pressure do not cause the flow to increase further.
Operating a valve at or beyond the choked point calculated from FL (∆pchoked) is almost sure to result in excessive noise and cavitation damage.
Cavitation damage prediction
The concern with cavitation is twofold: the potential for high noise levels and the potential for valve damage. Several reliable methods exist for predicting valve noise, including methods published by the International Electrotechnical Commission, the ISA and the German VDMA. No standard exists for predicting cavitation damage.
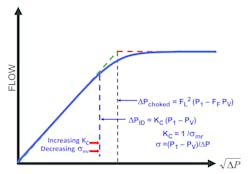
Some valve manufacturers predict the beginning of cavitation damage by defining an incipient damage pressure drop, which this author will call ∆PID, using a KC factor (see formula in Figure 5).
Figure 5. KC and o-mr as predictors of cavitation damage
Initially, valve manufacturers defined ∆PID and Kc as the point at which the actual flow curve deviates from a straight line by 2 percent. It was later determined that this was not necessarily coincident with the beginning of damage. Some manufacturers now evaluate actual application experience with cavitation damage and assign what are, hopefully, meaningful values of Kc to valves. One manufacturer uses a Kc for its stem-guided globe valves that is equal to 0.7, which it claims does a good job of predicting the point at which damage begins.
Other manufacturers, based on the recommended practice ISA–RP75.23–1995, Considerations for Evaluating Control Valve Cavitation, use sigma (σ) to represent various levels of cavitation. They use values of σmr (the manufacturer’s recommended minimum value of sigma for a particular valve). Sigma is defined as (P1 – PV) / ∆P. σmr and Kc are reciprocals of each other and convey similar information, though the recommended practice includes additional parameters. Higher values of Kc values move the point of incipient damage closer to ∆Pchoked, where lower values of σmr do the same.
FL is not a cavitation parameter but a choked flow parameter. Its only use is to determine the theoretical choked flow point based on the assumption that the choked flow point, ∆Pchoked, is the intersection of the two straight dashed lines shown in Figures 1 and 4 in red and green. Using FL as a cavitation parameter will likely result in unacceptable levels of cavitation damage.
Cavitation damage
Cavitation method history
The method for predicting cavitation damage with which the author is most familiar and that has been used with success for more than 25 years is based on the fact that the same thing that causes damage also causes the noise, namely the collapse of vapor bubbles.
The idea of correlating noise with cavitation damage surfaced in 1985 when Dr. Hans Baumann published an article in which he established a maximum sound pressure level of 85 A-weighted decibels (dBA) as the upper limit to avoid unacceptable levels of cavitation damage in butterfly valves.
Because the same number of bubbles per second that result in a sound pressure level of 85 dBA and present potential for cavitation damage in a 6-inch valve are more spread out and less concentrated in an 8-inch valve, more bubbles are allowed per second and hence a higher noise level is present in larger valves. Applying the same reasoning, the number of bubbles per second tolerable in a 4-inch valve would be more concentrated in a 3-inch valve, so to avoid damage in the smaller valve, the noise limit has to be lower.
The SPL limits established (based on noise calculations using VDMA 24422 1979), to avoid cavitation damage are:
- Up to 3-inch valve size: 80 dBA
- 4- to 6-inch: 85 dBA
- 8- to 14-inch: 90 dBA
- 16-inch and larger: 95 dBA
Note that regardless of the noise calculation, the actual pressure drop must be less than the choked pressure drop because experience shows that operating above the choked pressure drop is almost certain to result in damage in most control valve applications.
References
- This subject is discussed in ISA-RP 75.23-1995 "Considerations for Evaluating Control Valve Cavitation" Section B.8.7 and beginning with the last paragraph on page 41 of "Cavitation Guide for Control Valves" published by the US Nuclear Regulatory Commission and can be downloaded from osti.gov/servlets/purl/10155405.
- Chemical Engineering. March 18, 1985.
Jon F. Monsen, Ph.D., P.E., is a control valve technology consultant for Valin Corporation. He wrote the chapter on "Computerized Control Valve Sizing" in the ISA Practical Guides book on control valves and the book Control Valve Application Technology: Techniques and Considerations for Properly Selecting the Right Control Valve.