This is Part II in a four-part series based on the contents of the new textbook, "Control Valve Application Technology, Techniques and Considerations for Properly Selecting the Right Control Valve."
Part I: An Insider’s Guide to Valve Sizing & Selection
Process variability refers to any unwanted variation in whatever an operator is controlling — flow, pressure, temperature, level, etc. The reason it is important that these controlled variables do not significantly change is because they can appear as changes in the properties or quality of the end product.
If a variability problem is present, there are a couple of ways to address it. One strategy is to make the product exceed specification. For instance, the thinnest spots in a roll of paper are still thick enough. The problem lies in the idea of giving away free product, and in today’s competitive market, most cannot afford to do that.
If a poor-quality product is made, it will either need to be sold for less, recycled (run a hydrocarbon back through a column or reactor, or re-pulp a roll of paper), which uses energy and time and is therefore expensive, or just sell it and hope nobody notices. If customers discover they are getting a low-quality product, they will start buying from someone else.
Another potential result of excessive process variability is that in order to make an acceptable product, the average throughput must be reduced. There is also the potential for putting extra stress on the control valve, other valves, or other process equipment, which could result in otherwise unnecessary maintenance and unscheduled downtime. In any case, process variability can cost money.
There are a number of things that can cause excessive process variability including the following:
- Composition of incoming raw materials
- Composition of incoming additives
- Process equipment
- Process control design
- Inadequate mixing/agitation
- Ineffective tuning of control loops
- Improperly selected or poorly performing control valves
The end-users are concerned with all of the items on this list, but for this discussion the last one will be addressed. Roughly half the time there is a variability problem, it can be traced to the control valve.
For good control, a valve is required that:
- Has its flow characteristic selected to match the process
- Is properly sized
- Has good static and dynamic performance
In Part I of this article, the importance of selecting a valve with an inherent characteristic that matches the process and proper valve sizing was discussed.
An improperly selected inherent flow characteristic will result in a non-linear installed flow characteristic. The result is a system that will be difficult or impossible to tune for fast, stable response throughout the required flow range. On the other hand, a properly selected inherent flow characteristic will yield a linear, or nearly linear, installed flow characteristic, making it easy to tune the system for fast, stable response throughout the entire required flow range.
Furthermore, oversized control valves have trouble accurately adjusting the flow to the desired rate. Assuming two valves have the same amount of stickiness, a properly sized valve will be able to adjust the flow in smaller increments (versus an oversized valve) and therefore be able to control the flow more accurately.
Control valve performance also has a major impact on the valve’s contribution to process variability. The most important measures of performance are resolution (or sensitivity), dead band, and speed of response.
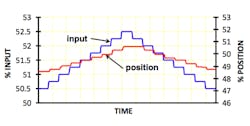
An example of a typical test for dead band and resolution is shown in Figure 1. The sticky behavior of valves is often referred to as "stiction." It is the result of the interaction between static friction and dynamic friction. Static friction is usually much higher than dynamic friction. As a result, a valve tends to stick in place until enough pressure builds up in the actuator to break the static friction, then the valve moves quickly to the new position. Resolution is a measure of the smallest movement that a valve is capable of in the same direction. This is called a static test, because one must always wait long enough after each step for any possible movement to take place. No measurements are made while the valve is moving, but only the valve’s static position is recorded after it has come to rest.
The control signal is stepped in one direction in very small steps. After each step there is a waiting period to make sure there is time for the valve to make any move it is going to make before the next step is initiated. Observing the number of control signal steps that are required to make the move indicates how sensitive the valve is, commonly referred to as "resolution."
After a number of steps in the same direction, the direction of the steps is reversed. Observing the number of steps required to initiate reversal of valve motion indicates what the dead band is.
In this example, the step size is ¼%. In the same direction, this valve responds to each ¼% step, so it has a sensitivity or "resolution" of at least ¼%. Upon reversal, it took two of the ¼% steps before the valve started moving in the reverse direction, so this valve has a dead band of no more than ½%. Dead band shows up in the process as dead time, which is destabilizing to control. Note that the scales for the input and position are different so that the two graphs will be easier to differentiate from each other.
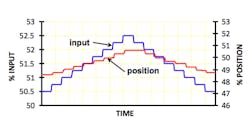
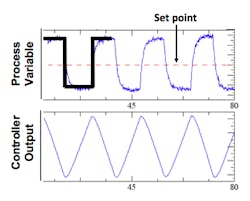
Figure 2 shows the test results for a very sticky control valve. The result of excessive stiction in a closed loop control system is a limit cycle and process variability. See Figure 3 for an example of a limit cycle. Look at the process variable trace in the figure and the horizontal line that has been drawn over the process variable trace at the left side of the graph. The valve is stuck and the process variable is above set point. The integral (or reset) action of the PI (Proportional plus Integral) controller ramps the controller output in an attempt to correct the error until enough pressure builds up in the actuator to break the static friction. Because dynamic friction is lower than static friction, the valve moves quickly to a new position. Before the static friction broke, enough pressure had built up in the actuator that the valve overshot the target position and the new process variable value is now below set point. As a result the PI controller reset action now starts ramping the controller output in the opposite direction in an attempt to correct the new error, but the valve is stuck again and does not move until enough pressure builds up in the actuator to break the static friction. The result is a "Limit Cycle."
The characteristic of a limit cycle is that the process variable oscillates in an approximate "square" wave fashion and the controller output oscillates in a "saw tooth" wave fashion. Loop tuning will change the period of the limit cycle, but will not eliminate it. The only fix for a limit cycle caused by a control valve is to repair or replace the valve.
Another important measure of control valve performance is the speed of response to step changes in the control signal. This is a "dynamic" test because it determines what the valve is doing while it is moving, and the entire movement is recorded.
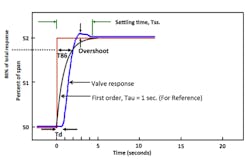
Figure 4 is a typical response of a valve to a step change in set point.
There will be some dead time (Td) before anything happens. There may or may not be overshoot.
In the past, two parameters were commonly used to measure speed of response, T63, the time required for the valve to respond through 63 percent of its total response, and T98, the time required for the valve to reach 98 percent of its final position.
T63 was chosen as being the equivalent of the time constant of a first order system. The word "time constant" was not used because control valve response is rarely first order.
For reference, a first order response with a T86 (two time constants) and settling time, similar to the T86 and settling time of the valve’s response, has been drawn in to emphasize that the valve response is not first order.
ISA S75.25.01, "Test Procedure for Control Valve Response Measurement from Step Inputs," now uses a single parameter, T86 (which corresponds to two time constants of a first order system). (Note that T86 is measured from the time of the step change in control signal.)
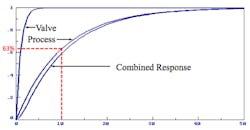
The speed of response of a control valve is also a concern. Figures 5 and 6 show the response of a first order system that has a time constant of 10 seconds, that is, a process that responds through 63 percent of its full response in 10 seconds.
Although control valve response is usually more complex than first order, it is allowable, for the sake of comparing the effect of valves with various speeds, to treat them as first order systems.
If the 10-second system were controlled by a valve with a 10-second time constant, the overall response would be as shown in Figure 5. The combined response is much slower than what the process is capable of by itself.
When the same 10-second process is controlled by a valve with a 1-second time constant, as shown in Figure 6, the combined response is nearly as fast as the speed with which the process could respond with an infinitely fast valve.
Typically, a valve that is five times faster than the process will have little effect in slowing the process from responding as quickly as it is capable of.
Below are some guidelines for valves in processes where very good control is required:
I. Resolution (stiction): ≤ 0.5%
II. Dead band: ≤ 0.5%
III. Speed of response:
A. Fast loops:
1. Valve Td ≤ 20% of desired closed loop process time constant
2. Valve T86 ≤ 40% of desired closed loop process time constant (This is equivalent to saying that the valve should be five times faster than the desired closed loop process response time.)
3. Valve settling time ≤ desired closed loop process time constant
B. Slow loops: Not important
IV. Step overshoot: 20% maximum
Twenty percent overshoot means 20 percent of the step size. For example, the overshoot for a 10 percent step should not exceed 2 percent of scale. The recommendation for T86 agrees with suggestions in the ISA valve performance technical report, ISA – TR75.25.02.
Figure 7 is included to demonstrate why the recommended speeds of response criteria make sense.
This is the same valve discussed earlier, and it just meets the above guidelines for a process where the desired closed loop time constant is 5 seconds.
The dead time is just under the recommended 20 percent of the desired closed loop time constant, meaning it is over in time to have little impact on the overall process response.
The valve reaches 86 percent of its full travel after only 40 percent of the desired closed loop time constant. It can be seen that the valve is way ahead of when the process needs to reach 63 percent of its final value, and even farther ahead of when the process needs to reach its two time constants (86 percent) value. Because the valve reaches 86 percent of its total response in 2 seconds, and the desired process response should reach 86 percent of its total response in 10 seconds, it is equivalent to saying that the valve is fives times faster than the desired process response time.
At the early stage of the full response, a small overshoot will contribute very little, if anything, to an overshoot in the process.
The valve response has settled to its final value after slightly less than one desired process time constant, long before the process is expected to reach its final value.
Things to remember:
- An oversized valve will make it difficult to adjust the flow precisely.
- A control valve with the wrong inherent flow characteristic will result in a non-linear installed flow characteristic and make it difficult or impossible to find a set of PID control parameters that give quick and stable control throughout the required flow range.
- A limit cycle is most likely caused by a valve that has excessive static friction (stiction) and needs to be repaired or replaced.
Jon F. Monsen, Ph.D., P.E., is a control valve technology specialist at Valin Corporation, with more than 30 years’ experience. He has lectured nationally and internationally on the subjects of control valve application and sizing, and is the author of the chapter on "Computerized Control Valve Sizing" in the ISA Practical Guides book on Control Valves. He is also the author of the book "Control Valve Application Technology: Techniques and Considerations for Properly Selecting the Right Control Valve."