This is Part I in a four-part series on energy saving strategies for evaporative cooling towers.
READ ALSO: Part II—How Changes in Flowrate Affect Cooling Tower Efficiency
A century ago steam engine operators discovered they could improve energy efficiency by adding a heat exchanger on the steam discharge. The idea was to flow ocean or river water through the heat exchanger lowering steam temperature and reducing the steam engine’s compression ratio. This worked well for marine applications, but was too costly for land-based systems where the only available water supply was from a municipality, as apparently the advent of the water meter preceded the steam engine. Evaporative cooling towers were invented to provide land-based efficient steam engine operation by recapturing the vast majority of the water used by the heat exchanger.
Cooling Towers 101
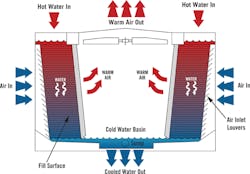
In general, evaporative cooling towers are used to cool process water via evaporation. Figure 1 shows a typical cross-flow evaporative cooling tower. A water pump forces high temperature process water to enter at the top through nozzles. The nozzles disperse the water onto a large surface area known as the fill. The fill’s only function is to efficiently delay the water reaching the bottom of the tower and allow more time for the air to interact with the process water. Gravity causes the water to slowly make its way through the fill while a fan forces air across the water path until it reaches the bottom of the tower (basin). The air passing through the tower causes some of the water to evaporate and give up heat. For every pound of water that evaporates, approximately 1,000 BTUs are removed. The air leaves the tower moisture laden and mixes with the atmosphere. Any water that is evaporated is made up by a fresh water measuring system located in the cold water basin. The cross flow tower shown in the illustration is very common. Even though there are many variations such as static (no fan), counter-flow and others, the common thread is cooling the process water using evaporation.
READ ALSO: Big Data — How Sensors Can Enable Precise Maintenance & Optimum Equipment Reliability
Cooling Tower Control Optimization Strategy
Evaporative cooling towers are usually designed to provide the proper cooling needed for the process when both production and the outdoor conditions are at their maximum. This is the only time when the cooling needs of the process actually match the capacity of the tower. This means that at all other times the tower has a greater capacity than the design heat load. As you may surmise, the vast majority of time either the air or water flow of the evaporative cooling tower can be reduced and energy can be saved. In many cases, facility owners quickly adopt the idea of varying fan speeds, as this is a fairly easy fix. In some cases, varying pump speed has the potential to save even more energy but it must be done with caution.
The question always comes down to what is the best strategy and how much will it save? To answer this question, there are four key variables that must be understood:
1. Process heat load
2. The Affinity Laws
3. Basic water flow science
4. Psychrometrics
Types of Cooling Tower Heat Loads
Process heat loads can be classified in two different ways, the simplest being one which derives no energy benefit from the tower water supply to the process being at a lower temperature than its maximum design, in which case the tower has a fixed set-point on the supply water temperature. In other words:
Total power = fan + pump
The more complicated process heat load is an application where the process energy efficiency is significantly improved by lowering the evaporative cooling tower supply water temperature to a certain point — like our previous example of a steam engine or refrigeration system, where the lower tower supply water temperature reduces the compression ratio, which results in lower energy use. In most cases, the power required for the process is far greater than the tower fan and pump combined. In these instances it makes sense to use more tower energy to achieve a lower tower supply water temperature because the improvement in energy use of the process is greater. This makes the optimization a bit more complicated because now the total power includes the process:
Total power = process + pump + fan
Since the process power changes dependent on what happens with the tower fan and pump, it is literally the difference between juggling three balls verses two. In these types of applications the goal is to always ensure that the sum of the power of the process, pump and fan are optimal at all times.
Measuring Cooling Tower Heat Loads
Figure 2. Pressure drop flow curve through a heat exchanger
The heat load the process has on the evaporative cooling tower starts with a very simple equation:
BTU/Hr. = GPM X 500 X TD
GPM is gallons per minute of cooling water going through the process heat exchanger while TD is the difference in temperature of the water entering and leaving the heat exchanger. The 500 factor is a constant made up of the amount of pounds per gallon of water (around 8.33), the specific heat of water (1) and 60 to convert minutes to hours. Therefore 8.33 x 1 x 60 = 499.8 or approximately 500. The nice thing about water is that, unlike air, the density doesn’t change much at normal temperatures and it has a specific heat of 1 BTU/lb. (which means it takes 1 BTU to raise the temperature of 1 pound 1 degree F.). However, some towers run when the temperature is below freezing, requiring anti-freeze (glycol) to be added to the water. Depending on the anti-freeze manufacturer, as well as its percentage in the water, it may not weigh 8.33 pounds per gallon and also have a slightly different specific heat. For example, if the glycol water mixture only weighs 92 percent as much as water (referred to as the specific gravity) and has a specific heat of .96 BTU/lb. then the calculation would be:
(8.33 X .92) = 7.66 Gal/lb. X .96 Sp. Ht. X 60 = 441.4
So instead of the 500 we used as a constant the new value would be roughly 441.
Taking glycol out of the equation, let’s say that you are cooling an oven with water entering at 78 degrees F and leaving at 85 degrees F using 100 gallons per minute flow. What would be the heat load? Using the formula of GPM X TD X 500 yields:
100 X (85-78) X 500 becomes 100 X 7 X 500 = 350,000 BTU/Hr.
Therefore, the heat load on the oven is 350,000 BTU/Hr.
Using this same example, what would happen if the flow changed to 90 gallons per minute and the heat load remained constant? If you said the temperature difference would change, you are correct. So now we recalculate and find the new temperature difference.
The formula is BTU per hr. / (GPM X 500), which becomes 350,000 / 90 X 500 = 7.8 degrees F. So lowering the flow rate by 10 percent increases the temperature difference by 0.8 degrees F.
So how can one determine what the heat load of the process is if no flowmeter exists? Quite often, heat exchanger manufacturers provide tables that relate flow to pressure drop as shown in Figure 2. By installing pressure gauges on both the inlet and outlet sides of the heat exchanger you can convert the pressure difference to flow rate to get a rough estimate of the flow.
For example, a model number E2209-B heat exchanger (yellow line), with a pressure drop of 10 feet of water column, the flow rate would be a little over 1,100 GPM. If your gauges read in lbs. per sq. inch (PSI), then this would be the equivalent of (10 / 2.31) around 4.4 PSI pressure drop since every PSI = 2.31 ft. if the process uses water with no glycol.
What if the Cooling Tower Application Uses Glycol?
If the mixture contains glycol, multiply 2.31 times the specific gravity to obtain the conversion. For example, if an application with glycol has a specific gravity of 90 percent (which means it weighs 90 percent as much as water) the conversion would be 2.31 X .9 or 2.079. Therefore:
10 / 2.079 = 4.81 PSI
What If There Is No Pressure Drop Table?
If no table exists, your options are to either install a flowmeter, which is what I would highly recommend, or rent a good portable ultrasonic meter. If a portable meter is used to determine flow, permanently mount pressure gauges on the inlet and outlet sides of the heat exchanger and develop your own pressure drop to flow chart within the proper flow range. This will serve to help future operators monitor the difference in pressure across the heat exchanger and have a rough idea if the flow is within the correct range. While you’re at it, install quality entering and leaving thermometers for the same reason.
It’s a Ton … Sort of
A common term used in specifying the capacity of heat removal in cooling towers is tons of cooling. In the early years of refrigeration, a good many of the applications were directed toward making ice. For those of you not old enough to recall, this was before most people had electric refrigerators and most everyone had iceboxes. I’m just guessing, but the refrigeration equipment salespeople at the time probably found it easier to tell customers how many tons of ice their equipment could produce a day rather than explain what a BTU was. A ton is therefore based on the amount of heat required to convert water into one ton of ice (2,000 pounds) in 24 hours. Since each pound of water converted to ice takes 144 BTU, the formula is 2,000 X 144 = 288,000 BTU. Therefore 1 ton of cooling is equal to 288,000 BTU/Day or 12,000 BTU/Hr. or 200 BTU/Min. or, if you like, 105,120,000 BTU/Yr.
Of course household refrigerators rapidly replaced the icebox and it went the way of the steam engine. When that happened, the need for ice plants also diminished. What was left behind was the term "tons of cooling," and to this day it is still a common term major manufacturers use in North America to describe the heat removal capacity of cooling equipment. Usually, when cooling equipment manufacturers speak the lingo of tons, they most often refer to the hourly amount, which is 12,000.
Again, I’m speculating, but the evaporative cooling tower salespeople got in on the act because refrigeration engineers realized that ice plants could run more efficiently if they used water cooled refrigeration systems. Now I suppose the tower salespeople didn’t want to find themselves explaining to customers what a BTU was any more than the refrigeration equipment sales guys. The problem is that even though the refrigeration systems removed a 12,000 BTU/Hr. to create ice, there was additional inefficient amount of heat added in the process by the refrigeration compressor. This inefficiency meant that cooling towers would not only need to remove the heat added by the ice but the compressor as well. So again, I’m guessing, but the tower salesperson probably did what any good salesperson would do — change the numbers. So, in the tower world a ton is not 12,000 BTU/hr. instead it is 15,000 BTU/hr. with the added 3,000 BTU for removing the compressor heat. So when a tower manufacturer says the tower is rated at 3 tons, he means 3 X 15,000 = 45,000 BTU/Hr.
Using our formula of BTU/Hr. = GPM X 500 X TD, how many GPM per ton would be needed to reduce cooling tower water from 95 degrees F to 85 degrees F to equal 1 tower ton?
Since a cooling tower ton is equal to 15,000 BTU/Hr. the formula is:
GPM = 15,000 / (500 X (95-85)) = 15,000 / (500 X 10) = 15,000 / 5,000 = 3 GPM
Therefore, an evaporative cooling tower with a 10-degree temperature difference between the tower entering and leaving water requires 3 GPM per ton.
Now that we have a basic understanding of heat loads, read "Part II: How Changes in Flowrate Affect Cooling Tower Efficiency" in which we discuss evaporative cooling tower fans and pumps.
John Pitcher is the CEO of Weber Sensors, a 50-year-old German manufacturer of flow products based on the calorimetric principle of operation. Previously he was the founder of Scientific Conservation, which was one of the first companies to use cloud computing for fault detection and diagnostics. Mr. Pitcher’s 40-year career covers many product development and leadership roles in the automation and energy efficiency fields. He can be reached at 770 592-6630 or [email protected].