Knowledge of the density of a fluid and its variation with temperature and pressure is essential for conversion between mass and volume. This is of particular importance in the oil and gas sector where many flow measurement systems make use of volumetric flow measurement devices, but mass is the quantity required for reporting production and for allocation in shared transportation systems.
Furthermore, crude oil and petroleum products are typically sold by volume at reference conditions (e.g., 60°F and 0 psig or 15°C and 101.325 kPa); hence, the effects of temperature and pressure on fluid density (volume) are required to convert from measured to reference conditions.
Direct measurement of the density of a fluid passing through a volumetric flow measurement device will, in principle, provide the lowest uncertainty when converting to mass flow. However, if the temperature and pressure at the density-measuring device differ from those at the flowmeter, errors will be introduced unless the temperature and pressure dependence of the fluid is sufficiently and accurately known.
The measurement task involved in determining the effects of temperature and pressure for all crude oils and refined products traded globally would be immense. Therefore, alternative approaches have been developed, in particular, correlation methods applicable to generalized product groups. For crude oil and refined products, the most widely used approach involves the volume correction factors (VCFs) maintained by the American Institute of Petroleum (API). These factors are widely used throughout the oil industry, including being programmed into the flow computers that form a fundamental part of fiscal flow measurement systems.
However, recent commissioning of the new high-pressure single-phase oil calibration facility at TUV SUD NEL’s elevated pressure and temperature (EPAT) facility has provided evidence of problems with the use of the standard method of calculating oil density at elevated pressures. Significant bias errors were observed when compared to traceable experimental density measurement of the oil samples concerned. This has potentially wide-ranging impact across the entire industry and requires urgent attention.
Accurate values of the densities of the oils used in TUV SUD NEL’s flow measurement facilities are essential for ensuring that each facility meets its overall accredited uncertainty. Previously, when the facilities were operating at close to ambient pressure, the use of generic compressibility correction factors were sufficient to account for the changes in density with pressure. Now, with the wet gas facility operating at up to 63 bar, the EPAT facility operating at up to 100 bar and the advanced multiphase facility planned to operate at up to 140 bar, the use of generic compressibility correction factors would lead to potential errors in calculated oil densities in excess of 0.25 percent, rather than the 0.02 to 0.03 percent required.
Correction factors to account for the thermal expansion of liquid hydrocarbons were first formally developed by the U.S. National Bureau of Standards in 1916. The data used to develop these VCFs were mainly derived from measurements made on samples from U.S. domestic oil production in 1916.
A compressibility standard for hydrocarbons was developed in 1945 for the API, based on limited data obtained mostly from pure compounds and lubricating oils. In 1945, the U.K. Institute of Petroleum (IP) also published VCF tables, and in 1952, the British and American temperature correction factor tables were joined together. These tables were called the Petroleum Measurement Tables and were published jointly by the American Society for Testing and Materials (ASTM), the API and the IP. They are commonly referred to as the 1952 Tables or "Blue Book Tables."
Major revisions of the standard were issued in 1980 and 2004. In 1981, a revised compressibility standard was developed. Although based on a broader database, the limits of the experimental data were from 681 to 934 kgm-3, 0°C to 150°C and 1 to 50 bar(a), but the standard allowed extrapolations, in particular, up to 104 bar(a).
For the purpose of calculating VCFs, the API method classifies petroleum fluids as:
- Crude oils
- Refined products
- Lubricating oils
An additional category of "Special Applications" included use when:
- "The generalized commodity group’s parameters are suspected of not adequately representing the thermal expansion properties of the liquid."
- "A precise thermal expansion coefficient can be determined by experiment."
While there are several sets of coefficients to account for thermal expansion, depending upon the liquid’s classification and density at 60°F, there is only one set of coefficients to account for compressibility for all fluids, regardless of classification. While this generalization may have been adequate for the original purpose of the tables, recent work has shown that it can introduce significant errors for fluids that do not fall within the compressibility ranges of the fluids used to derive the original correlations.
To explicitly examine potential limitations of the API VCF method, the densities of four of the oils used in TUV SUD NEL’s flow measurement facilities were measured at temperatures between 10°C and 75°C, at pressures from 1 to 101 bar(a) and the results compared with calculated values. For each oil, the calculations were done by treating it as a crude oil — a refined product and a special fluid in turn.
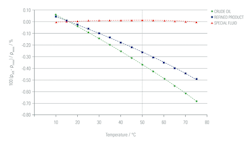
For all four oils, the trends are broadly similar. At the reference temperature of 15°C, all three methods produce good results for the four oils, and when calculated as a special fluid, the results are good across the temperature range, as would be expected since the user-defined thermal expansion coefficients have been derived from the experimental data. However, when treated as either a generalized refined product or a generalized crude oil, all four oils display significant errors as the temperature is changed from the reference value of 15°C, with errors of up to -0.70 percent.
Figure 1. An example of the percentage difference between the calculated and measured densities for one of the oils at 1 bar(a) for the three calculation methods. Figures courtesy of TUV SUD NEL
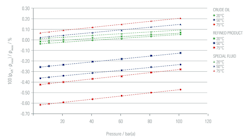
Figure 2. The results for one of the oils at elevated pressure, plotting the percentage differences between the calculated and measured densities for each of the three calculation methods
For all four oils, the smallest errors are obtained when they are calculated as a special fluid, because this essentially removes the temperature-dependent errors generated when treating them as generalized crude oils or generalized refined products. However, all four oils show the same trend of monotonic increases in errors with pressure, regardless of the calculation method used, with errors ranging from -0.6 to 0.2 percent.
The TUV SUD NEL EPAT facility uses a volume-based device as its flow rate reference system, but is normally used to calibrate Coriolis flowmeters, which measure mass flow rates. Accurate knowledge of the density of the fluid passing through the reference measurement system and the device being calibrated is therefore essential. In view of the potential errors, use of generic expansion coefficients would not be acceptable for this application.
As TUV SUD NEL is able to measure the density of the fluids used in its flow measurement facilities with an uncertainty of 0.025 percent across the temperature range from 10°C to 90°C, at pressures up to 90 bar(a), an alternative approach is possible. For each fluid, the experimental data are fitted to an equation that enables the density to be calculated at any temperature and pressure with an overall uncertainty (combining the uncertainty of the experimental data and the fitting process) of 0.04 percent. For EPAT, for example, this allows the facility to meet its overall uncertainty of 0.08 percent for mass flow rate, as the volumetric reference system has an uncertainty of 0.03 percent.
Unfortunately, due to the large amount of data required to optimize the coefficients for the form of equation used by TUV SUD NEL, this approach is not ideal as a general replacement for the use of VCFs. For applications where mass flow rates are required, the use of suitably calibrated Coriolis flowmeters would avoid this problem; however, correct calibration of the Coriolis flowmeter is essential. If the meter is calibrated against a volumetric reference system using VCFs, errors in excess of 0.2 percent could still occur. For a field producing 50,000 barrels of oil per day (and an assumed oil price of $70 a barrel), this would equate to a potential financial exposure of £2 million per annum.
Although the use of Coriolis flowmeters will provide a good solution in many situations, for some applications, knowledge of the density of a fluid and its variation with temperature and pressure is essential. To ensure the lowest financial exposure, direct measurement of fluid density or the use of a suitable equation with optimized coefficients should be considered. Traceable calibration of the density measurement device and validation of the equation form and its coefficients are also vital.
Conclusion
Although it is often overlooked, knowledge of the density of a fluid and its variation with temperature and pressure is vital for many flow measurement applications. As such, the determination and use of density data should be accorded the same care and attention that is given to flow measurement.
Norman Glen is a service leader for densitometers and physical properties of fluids at TUV SUD NEL, a provider of technical consultancy, research, testing and program management services. Part of the TÜV SÜD Group, TUV SUD NEL is also a global center of excellence for flow measurement and fluid flow systems and is the U.K.’s National Measurement Institute for Flow Measurement.